2020年12月16日，爱游戏平台 王學欽教授團隊與美國耶魯大學公共衛生學院的Heping Zhang教授合作在美國科學院院刊《PNAS》在線發表題為“A polynomial algorithm for best subset selection problem”的研究論文， 針對線性回歸模型的基準問題——最優子集選取，提出了一種快速算法。

發現事物間的關係是大部分科學研究的目的，這在統計學中稱之為回歸分析。其中，線性回歸模型由於其簡潔性和可解釋性而成為最有用的科學研究工具之一。盡管線性回歸模型被如此廣泛的使用，但其中一個很基本的問題：如何在一組變量中選擇最優的子模型，尚未解決。這個問題的求解被認為是NP-hard問題。得益於現代科技的發展，數據的收集變得越來越便利，在典型的生物醫學研究中會收集到上百個變量，常規的全基因組研究中則涉及到成千上萬甚至是百萬級別的遺傳變異。現有的算法難以在上萬級別的實際問題中尋找到最優子集。

為了解決這個問題，王學欽團隊利用排序和剪接的思想結合一個新的信息準則發展出一種新的算法，使得算法在有限步內就能得到穩定解；並證明了在一定條件下，依大概率，該算法具有多項式的時間複雜度，而且能夠選出最優子集。

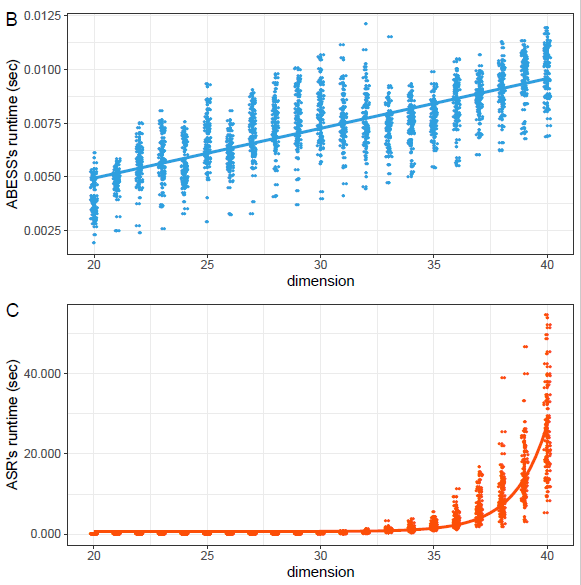
圖一 算法的計算時間隨著變量個數增加的散點圖。其中上圖是新提出的算法，下圖是經典的最優子集選取算法。

中國科學技術大學王學欽教授和耶魯大學Heping Zhang教授為論文的共同通訊作者，中山大學博士生朱俊賢和中國科學技術大學溫燦紅特任副研究員為論文的共同第一作者。該研究得到了國家重點研發項目，國家自然基金委項目和安徽省自然基金委項目等資助。

論文鏈接：https://doi.org/10.1073/pnas.2014241117